UVa 1312 Cricket Field 解题报告(枚举 + 离散化)
1312 - Cricket Field
Time limit: 3.000 seconds
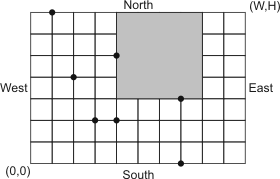
Once upon a time there was a greedy sovereign who mandated by greed neither allowed alterations nor any modifications of design plans within his park. Mandated by greed, the king refused to listen to the architect’s plans which had proposed constructing an idealistically conceived cricket ground at precise center surrounded by neatly arranged native trees and featuring inviting walkways lined with evergreen hedges for spectators. Instead, he ordered neither to cut nor to plant even a single tree in his park but demanded an enormous cricket field solely for personal enjoyment. Should the architect dare to make any changes or propose a smaller area where such an endeavor might become feasible then he would face severe consequences. Moreover, he demanded immediate submission of detailed design blueprints pinpointing exact location and dimensions of intended cricket ground.
Your objective is to assist poor Architect in alleviating his headaches by creating a program designed to calculate the largest feasible area of a cricket field and its precise location within the park boundaries, all while meeting King's requirements.
The matter is somewhat simplified by considering that King's Park assumes the shape of a rectangle and is settled upon flat terrain. Furthermore, its boundaries are precisely aligned along the North-South and East-West axes. At the same time, royal cricket is traditionally played on a rectangular field that also conforms to these cardinal alignments. A Cartesian coordinate system has already been implemented by the architect to precisely determine every tree's location within this system. Of course, this coordinate system aligns perfectly with North-South and East-West directions. The Southwestern extremity of the park holds coordinates (0, 0), while its northeastern boundary marks (W, H), where W represents the park's width in feet and H denotes its height.
For this task, it is permissible to disregard the diameter of the trees. Trees must not be located within the cricket field but can instead be positioned adjacent to it. The cricket field may also abut the park's boundary but must not extend beyond it.
Input
The input commences with a single positive integer positioned alone on a line, serving as an indicator for the number of subsequent cases. Each case is described in detail below. Following this initial line, an empty line separates the cases. Additionally, there is another empty line between consecutive inputs.
在输入文件的第一行包含三个整数_N_, W, 和_H_, 用空格分隔。例如, 当_N_=0时

N

- is the number oftrees in the park. W and H (1

W ,H

10000)are the park width and height in feet respectively.
随后的_N_行将描述公园内树木的坐标信息。每行包含两个整数值_X_i和_Y_i,它们之间以一个空格分隔(0)

X i

W ,0

Y i

H) represents the coordinates of the i-th tree in the set H. Each tree is uniquely positioned in the coordinate system.
Output
For each trial case, the result should adhere to the document or specification outlined in this section. The results of consecutive trials must be separated by a single space.
Output to the specified file a single line containing three integers: P, Q, and L. Here, (P, Q) denote the coordinates of the cricket field's southwestern corner. Additionally, L represents the length of each side of this field. It is important to note that if multiple valid field configurations exist, particularly those with the maximum possible area, any one of them should be provided as output.
Sample Input
Sample Output
Note: That is a sample inputs and outputs that corresponds to the park plan that is shown on the picture.
解题报告: 经典题目。找出最大空白方形。
注意到长度和宽度均稍大于1 \times 1e4的情况下(即1万),直接穷举所有的可能矩形边框必然会超出时间限制范围(Time Limit Exceeded, TLE)。然而由于仅有100棵树的存在(即n=1e2),我们可以将问题空间转换到二维平面中的离散化表示上进行求解。具体而言,在二维平面上遍历可能存在的矩形顶部和底部y坐标值(即所谓的"上下"y范围),然后再依次对每一棵树进行检查:如果该棵树的高度恰好落在当前遍历到的一个矩形高度区间内,则将其x坐标的左端点更新为当前所考察的新左边界;直到找到下一个满足条件的新左边界为止,并相应地更新当前最优解的答案值(即最小面积)。这种方法的时间复杂度为O(n^3)量级(其中n为节点总数)。特别地,在整个图像区域的实际边界的处理上需要注意这一点:实际边界的某些区域被认为也是被占用了空间的位置(比如虚设了外围围栏),因此在计算过程中必须对此进行适当的处理以避免遗漏潜在的有效矩形区域。
代码如下:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <vector>
#include <queue>
#include <map>
#include <set>
#include <string>
using namespace std;
#define ff(i, n) for(int i=0;i<(n);i++)
#define fff(i, n, m) for(int i=(n);i<=(m);i++)
#define dff(i, n, m) for(int i=(n);i>=(m);i--)
#define mem(a) memset((a), 0, sizeof(a))
typedef long long LL;
typedef unsigned long long ULL;
void work();
int main()
{
#ifdef ACM
freopen("in.txt", "r", stdin);
// freopen("in.txt", "w", stdout);
#endif // ACM
work();
}
/*****************************************/
struct Point
{
int x, y;
bool operator<(const Point & cmp) const
{
return x < cmp.x;
}
} p[111];
int n, w, h;
int xx, yy, len;
int y[111];
void solve()
{
sort(p, p+n);
y[n] = 0, y[n+1] = h;
sort(y, y+n+2);
int m = unique(y, y+n+2) - y;
len = 0;
ff(a, m) fff(b, a+1, m)
{
int miny = y[a];
int maxy = y[b];
int dy = maxy - miny;
if(dy <= len) continue;
int sta = 0;
ff(i, n)
{
if(p[i].y > miny && p[i].y < maxy)
{
if(len < min(dy, p[i].x - sta))
{
len = min(dy, p[i].x - sta);
xx = sta;
yy = miny;
}
sta = p[i].x;
}
}
if(len < min(dy, w - sta))
{
len = min(dy, w - sta);
xx = sta;
yy = miny;
}
}
}
void work()
{
int T;
scanf("%d", &T);
fff(cas, 1, T)
{
scanf("%d%d%d", &n, &w, &h);
ff(i, n) scanf("%d%d", &p[i].x, &p[i].y), y[i] = p[i].y;
solve();
printf("%d %d %d\n", xx, yy, len);
if(cas != T) puts("");
}
}
代码解读